Project 2: Filters and Frequencies

Part 1.1: Convolutions from Scratch

Using the definition of convolution:

for result_i in range(result.shape[0]):
    for result_j in range(result.shape[1]):
        total = 0
        for i in range(ffker.shape[0]):
            for j in range(ffker.shape[1]):
                total += img[result_i + i, result_j + j] * ffker[i, j]
        result[result_i, result_j] = total
return result

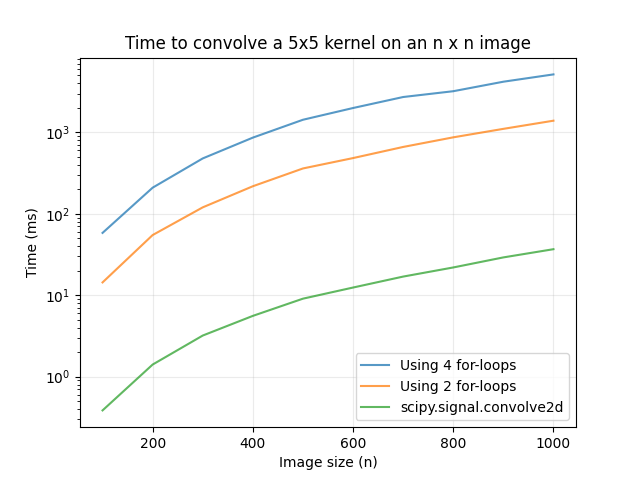
where ffker is the xy-flipped kernel and result is the output 2D array, we can slightly speed up the computation by replacing the 2 inner for-loops with result[result_i, result_j] = np.dot(img_flat, ffker.flatten()), where img_flat is the flattened 1D array of the current patch of img based on the position of the kernel. Although this optimization produces a noticeable speed-up compared to using 4 for-loops, the fastest way is still to use scipy.signal.convolve2d. Below is a timing comparison of the 3 methods above using a 5x5 kernel:

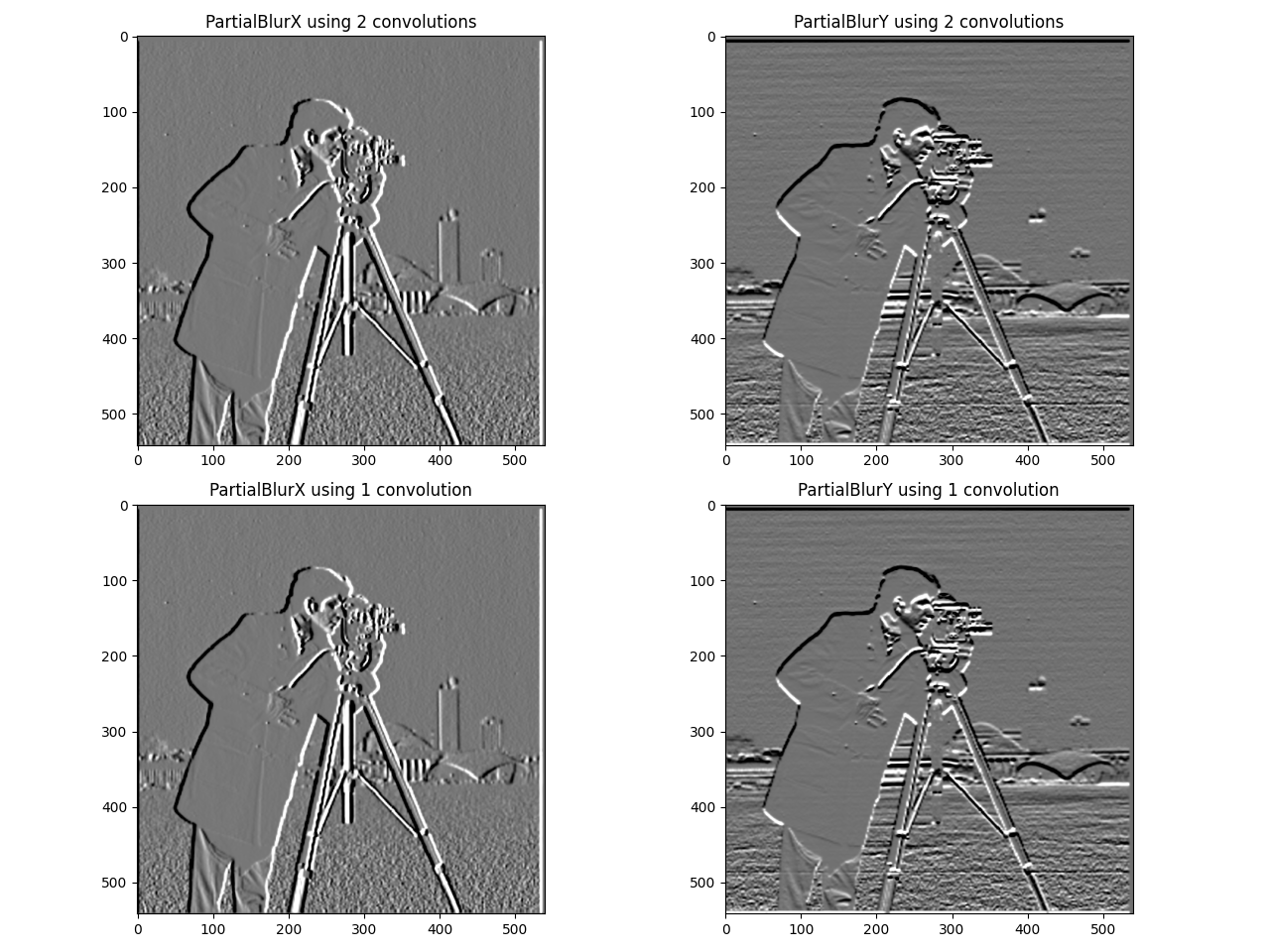
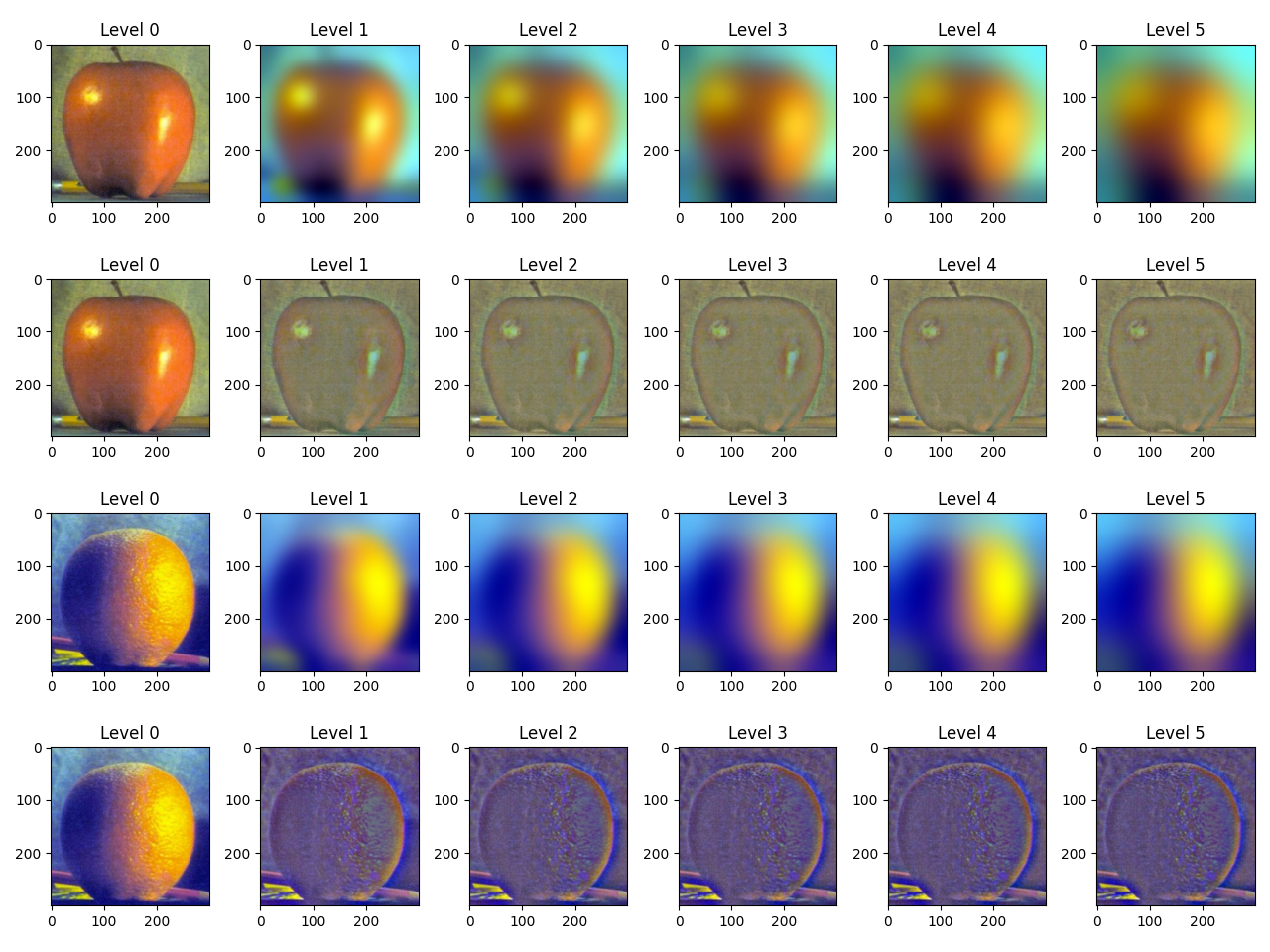
To demonstrate an application of convolution, we can convolve an image with the box filter, a kernel with entries that sum to 1 that contains only 1 unique value. We can also convolve with the difference operators 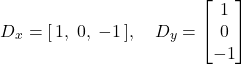for edge detection. Each kernel computes the difference in the x- or y-direction, so edges where the brightness of the pixel changes significantly will show up as white and black pixels on the output. Using box_9x9 = J₉ / 9² as the box filter, we get the following results:

For convolving with D_x and D_y, we have:

To handle boundries, we can set all of the padding pixels to 0, similar to the following:

if mode == 'valid':
    return convolve(img, ker, naive)
elif mode == 'same':
    pad_ht = (ker.shape[0] - 1) // 2
    pad_wl = (ker.shape[1] - 1) // 2
    img_padded = np.zeros((img.shape[0] + ker.shape[0] - 1, img.shape[1] + ker.shape[1] - 1))
    img_padded[pad_ht:pad_ht + img.shape[0], pad_wl:pad_wl + img.shape[1]] = img
    return convolve(img_padded, ker, naive)
elif mode == 'full':
    pad_h = ker.shape[0] - 1
    pad_w = ker.shape[1] - 1
    img_fpadded = np.zeros((img.shape[0] + 2 * pad_h, img.shape[1] + 2 * pad_w))
    img_fpadded[pad_h:pad_h + img.shape[0], pad_w:pad_w + img.shape[1]] = img
    return convolve(img_fpadded, ker, naive)
else:
    raise ValueError('Unsupported mode: ' + str(mode) + '. Must be one of \'valid\', \'same\', or \'full\'.')

A zero-valued pixel, however, is equivalent to a black colored pixel on the image. This means the function would introduce a dark edge if one wants to have the image be the same size after convolving, which is visible above. To prevent this scenario, the safest way is to let the first row/column be the first padding row/column on the top left side, and perform the same with the last row/column on the bottom right side. This process can also be carried out for the 2nd/2nd-to-last row/column, and so on. Compared to other approaches like 'wrap', this method ensures that there won't be significant artifacts by ensuring the padded pixels come from the closest pixels in the image. To implement this method, we can set the boundary variable to 'symm' in convolve2d. In comparison, the zero-padding mode is the same as the default mode in convolve2d, which shows how convolve2d has more functionalities than the naive implementation.

Part 1.2: Finite Difference Operator

Given the following image:

we can convolve this image with D_x and D_y to get the partial derivatives in the x- and y- direction. Using np.dot, we can then compute the gradient magnitude as follows:

Although the edges are visible, it's not clear, especially in the magnitude image. This is because when convolving an image with channel values in the range [0, 255], the resulting image will have a range of [-255, 255], so normalizing the image directly makes the overall image darker. To reduce the noise of the non-edge pixels, we can set a limit for each channel value before normalizing. Using a threshold of 25% from both sides, we get the following result:

From the image above, the edges in the gradient magnitude image are brighter and more distinct.

Part 1.3: Derivative of Gaussian (DoG) Filter

To further improve edge visibility, we can first smooth out the noise by convolving the original image with a Gaussian filter. To generate one with dimensions n × n, we can take the outer product of 2 length n arrays. Below is the result of blurring the original image using a 5 × 5 Gaussian filter with σ = 1:

Applying the same edge detection process above, we get:

To illustrate the improvements, below is a side-by-side comparison of the edge magnitudes for each of the 3 methods, in row-major order from least to most clarity:

Instead of applying 2 convolutions to the image, we can take advantage of the fact that convolution is commutative, and first convolve the Gaussian with D_x and D_y, then convolve the image with the resulting kernel. This optimizes the computation by only convolving with the image once. Below are the respective results:

Part 2.1: Image "Sharpening"

Using convolution, we can also sharpen a blurry image with a similar technique. Since a Gaussian filter removes the highest frequencies in a signal, subtracting the filtered image from the original would leave all of the highest frequencies from the base image. We can then add this difference to the original to highlight the highest frequencies of the image, then clip it to [0, 255] to preserve brightness. Using the following Taj Mahal image:

We can obtain the blurred and high-pass filtered versions of this image as follows:

Now, we can add the second image to the original to get a sharpened version:

In general, we can change the sharpening amount by multiplying the high-pass filtered image by a constant. Below is a demonstration of various sharpening amounts from 1 to 100:

From the visualization above, increasing the sharpening amount highlights the high-frequency signals from the original image. Below is an example of sharpening a blurred image, using the same selfie from 1.1 as the original image, and the box-filtered version as the starting image to sharpen:

Part 2.2: Hybrid Images

A hybrid image is when 2 images, one under a low-pass filter and the other a high-pass filter, are blended to create an illusion where one sees mostly the high-frequency image at a close distance, but only the low-frequency image at a longer distance. This occurs because our vision has a limited spatial frequency resolution, so higher frequencies fall outside of the frequencies visible at a sufficiently far distance. Below is an example of 2 images that we can align and create a hybrid effect:

To find the optimal σ for each image to create the Gaussian & impulse filter with, a good starting point through experimentation is 1.8-3% times the shorter of the width and height of the LPF image, and 0.6-1.5% for the HPF image. In the example above, a cutoff percentage of 3% and 1% was used:

Below is a visualization displaying the log magnitude of the Fourier Transform of the starting and the filtered images:

After aligning and combining the LPF and HPF images, we get the final result below:

This effect can also be used on any 2 images that are aligned, like the following examples, which use a frequency cutoff of 2% and 0.8% times the shorter side:

Part 2.3 & 2.4: Multiresolution Blending

To blend 2 images, we can first start by creating a Gaussian/Laplacian stack. This is similar to a Gaussian stack, except that at each level, we don't need to downsample. The easiest way to achieve this is to have a function that takes in an array of images, and for each level, append one image to a list and recurse on the last (latest added) element of the list. In the end, a 3D (4D if using RGB images) array will be returned that is a collection of all the images in the stack: